カーブでは内側と外側の長さがちがう

　リニアの軌道の幅は3.3m(*)です。カーブで軌道の内外でどのくらいの差ができるかという問題。

　半径8000mの円形の軌道を一周する場合。

A=(8000+3.3/2)×2×3.14=50250.362
B=(8000-3.3/2)×2×3.14=50229.638
A-B=20.724

　外側と内側の長さが約20mちがってきます。

　半径8㎞で90度方向を変えるカーブの場合は4分の1周ですから：

外側の長さは、12562.5905
内側の長さは、12557.4095

　ガイドウェイの側面に取り付けるパネルの長さは 12.6m。カーブの内外でそれぞれ何枚のパネルが必要か計算すると。

外側は、997.0309920634921枚
内側は、996.6198015873016枚

　パネル996枚分の長さは、12549.6mです。軌道外側の長さとの差は、12.9905m 足りません。パネルをもう1枚加えることができそうです。しかし、内側では、7.8095m でパネル1枚分はありません。内外ともにパネルの数をそろえないといけないので、パネルの数は996枚です。

　外側、内側ともにパネルの隙間の数は、996 です。外側では長さの足りない分を996で割ると 0.0130426706827309m。内側では 0.0078408634538153m。それぞれ、約1.3cm と約0.8cm です。

　12.6mというパネルの長さは、実際には12m58cmのパネルを12.6mごとに置くという意味だと思います(下図)(そういう規格になっているとでもいうのでしょうか)。パネルの間に2㎝のゆとりをとっているのだと思います。約1.3cm と約0.8cm なら、つまり半径8000mのカーブであれば、2㎝の範囲で、位置を少しずつずらせば解消できる(ごまかせる)のかなと思います。

        |←      12m60cm     →|
        | |==================| |
          |←    12m58cm   →|

しかし…

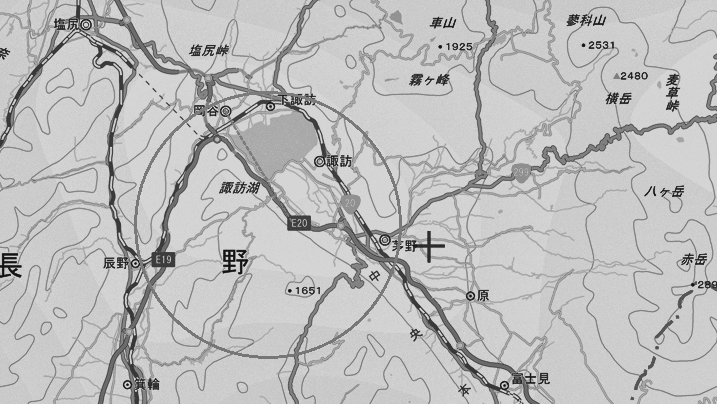
　カーブでクエンチ等が起きた場合の対処方法はなかなか難しいはず。12㎞にもなる連続するカーブを走るのは、超電導リニアの技術としては、挑戦的なことだと思います。だから、「ルート変更」という言葉で誰もが思いつく、諏訪湖付近を通過して伊那谷や木曽谷に下るルートは、とても無理だろうと思います。つまり、JR東海としては、「ルート変更」イコール「計画の断念」のはずです。

　リニアの本線上の一番急なカーブは半径8000m。諏訪湖付近ではこの半径8000mのカーブで120度近く方向転換しなくてはなりません。

* "研究展望：浮上式鉄道ガイドウェイの研究と技術開発",橋本渉一,土木学会論文集No. 619/1-47, 1-12, 1999・4,p3